소수 찾기 – 에라토스테네스의 체

에라토스테네스의 체란?

고대 그리스 수학자 에라토스테네스가 2에서 주어진 숫자까지의 소수를 찾는 방법으로 발견했습니다.

2부터 주어진 숫자까지 모든 구간의 숫자를 나열하는 것을 원칙으로 하고,

2에서 시작하여 찾은 소수의 배수를 제거하여 소수를 찾습니다.

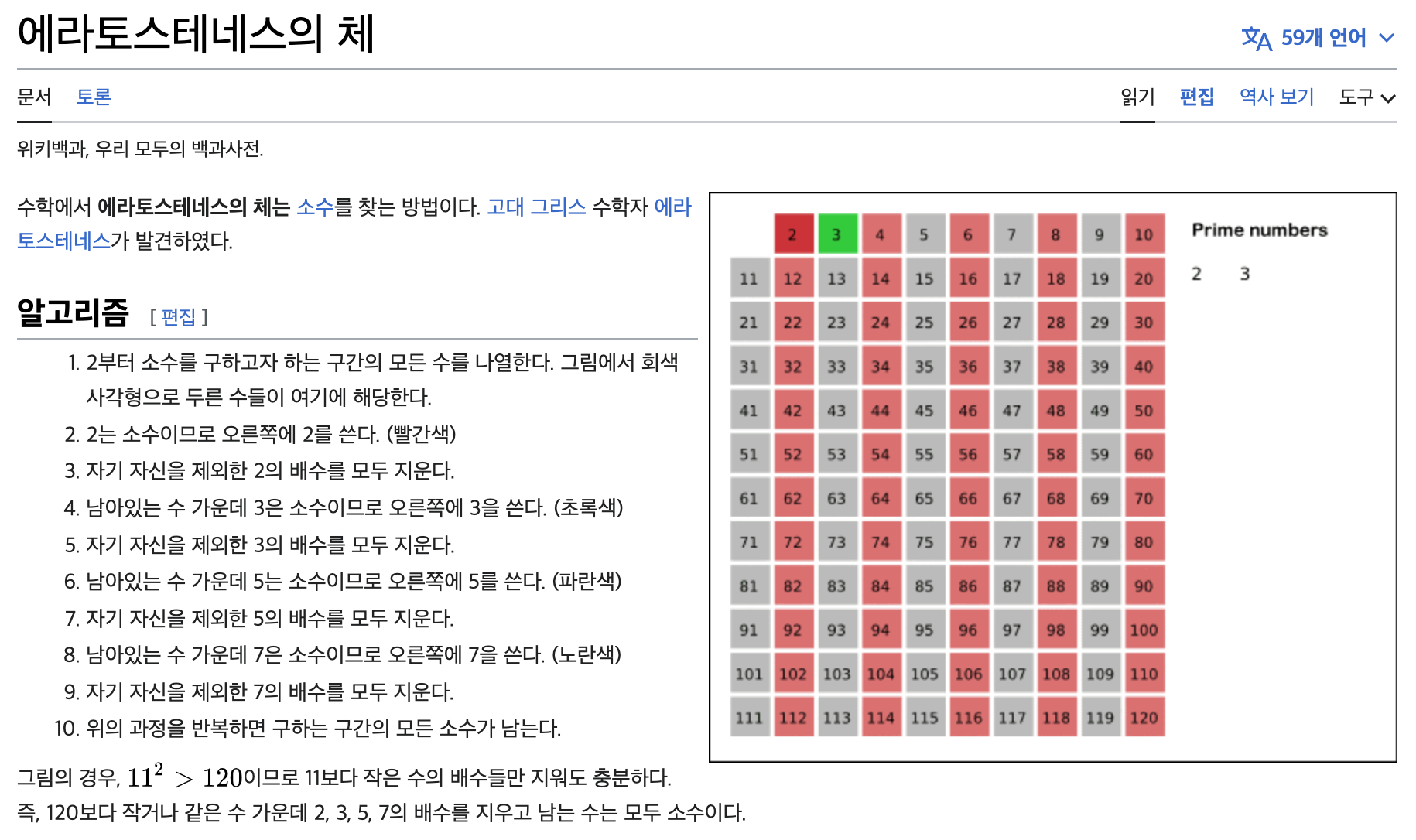
이를 수행하는 방법에 대한 자세한 내용은 Wikipedia에서 찾을 수 있습니다. – (링크)

암호

1. 본인을 포함하지 않는 경우

def prime_list(n):
  # 에라토스테네스의 체 초기화: n개 요소에 True 설정(소수로 간주)
  sieve = (True) * n

  # n의 최대 약수가 sqrt(n) 이하이므로 i=sqrt(n)까지 검사
  m = int(n ** 0.5)
  for i in range(2, m + 1):
    if sieve(i) == True:           # i가 소수인 경우
      for j in range(i+i, n, i): # i이후 i의 배수들을 False 판정
        sieve(j) = False

  # 소수 목록 산출
  return (i for i in range(2, n) if sieve(i) == True)

101을 출력할 때 다음과 같이 표시됩니다.

print(prime_list(101))
# (2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97)

101도 포함하려면 m을 계산할 때를 제외하고 각 n이 사용되는 곳에 +1을 추가할 수 있습니다.

2. 본인 포함

def prime_list(n):
  # 에라토스테네스의 체 초기화: n개 요소에 True 설정(소수로 간주)
  sieve = (True) * (n + 1)

  # n의 최대 약수가 sqrt(n) 이하이므로 i=sqrt(n)까지 검사
  m = int(n ** 0.5)
  for i in range(2, m + 1):
    if sieve(i) == True:           # i가 소수인 경우
      for j in range(i+i, n+1, i): # i이후 i의 배수들을 False 판정
        sieve(j) = False

  # 소수 목록 산출
  return (i for i in range(2, n+1) if sieve(i) == True)

+ 대상이 소수인지 확인

위에서 논의한 바와 같이 에라토스테네스의 체는 주어진 숫자까지의 소수를 찾는 방법입니다.

주어진 숫자가 소수인지 확인하는 방법이 궁금하다면 다음과 같이 확인할 수 있습니다.

암호

def check_decimal(n):
  # n의 최대 약수가 sqrt(n) 이하이므로 i=sqrt(n)까지 검사
  m = int(n ** 0.5)
  for i in range(2, m+1):
    if n % i == 0:
      return False
  return True

유사하게, n의 최대 약수는 sqrt(n), 즉 n의 제곱근보다 작거나 같기 때문에,

i를 제곱근 이하로 조사하여

2에서 n까지 모든 것을 비교하는 것보다 훨씬 더 많은 리소스를 절약할 수 있습니다.

* 101을 체크할 때 2~100을 모두 체크하는 것이 아니라 2~10만 체크하면 된다는 뜻입니다.

소수 확인은 종종 다른 알고리즘과 함께 사용됩니다.

말하자!